诺贝尔物理学奖解读——彭罗斯与他的时空奇点研究
蔡荣根 (中科院理论物理研究所) 曹利明 (中国科学技术大学物理学院)
李理 (中科院理论物理研究所) 杨润秋 (天津大学理学院量子交叉研究中心)
一、引言
北京时间10月6日晚,总奖金为1000万瑞典克朗(约合760万人民币)的2020年诺贝尔物理学奖在众人瞩目中揭晓:其中罗杰·彭罗斯(Roger Penrose)因为其“发现黑洞是广义相对论的必然预言”而获得一半的奖金。奖金的另外一半则授予莱因哈德·根泽尔(Reinhard Genzel)和安德里亚·格兹(Andrea Ghez),因为他们“在银河系中心发现了一个超大质量的致密天体”。
彭罗斯的学术成就极为全面,跨越了数学、物理学和哲学多个领域。事实上在获得诺贝尔奖之前,彭罗斯就在数学领域和物理学领域享有极高的声誉。现年已经90岁高龄的彭罗斯是广义相对论研究领域最为杰出的专家之一。彭罗斯与以往其他的诺贝尔物理学奖获得者有一个显著不同。以往大多数诺贝尔物理学奖获得者都是从事物理或者工程技术方面研究出身,但是彭罗斯步入学术研究的起步却是从事非常抽象的代数几何的研究。彭罗斯的数学天赋极高。在上个世纪50年代末,受到剑桥大学广义相对论研究专家Bondi和Sciama的影响,彭罗斯开始了广义相对论方面的研究。拥有纯数学的研究背景使得彭罗斯考察广义相对论的方式和当时的许多物理学家有所不同,并最终在广义相对论的理论发展方面做出了巨大贡献。这其中和这次“诺奖”关系最大的就是他关于“时空奇性”的若干研究和“宇宙监督假设”。这里我们做一些简单介绍。为了能够以最为通俗的方式让读者理解相关内容,我们在不至于导致谬误的基础上将不得不牺牲一些严谨性。希望对相关话题进一步深入了解的读者可以参阅文章中所列举的一些参考文献。
二、奇点定理
爱因斯坦的广义相对论将引力和时空的弯曲联系起来,这一理论在被提出之后的一百多年的时间里经受住了无数的实验检测。在广义相对论建立的早期,由于人们对这一充满革命性的理论知之甚少,因此人们在探索这一个理论的过程中也曾遇到过许多“困惑”。广义相对论中的爱因斯坦引力场方程是一个高度耦合的非线性方程。对这种方程的求解是一个极为困难的事情。在早期人们只能够求解一些具有高度对称性的情况。这其中最早的一个结果就是由德国的物理学家施瓦西(Schwarzschild)在广义相对论提出后一个月得到的真空球对称解——施瓦西解。另外一个同样著名的成果则是由俄国的物理学家弗里德曼(Friedmann)在1922年得到的,它描述各向同性均匀宇宙演化的弗里德曼-勒梅特-罗伯逊-沃尔克度规。虽然这两个解描述的物理非常的不同,但是人们发现它们有一个特别的相似之处:它们都表明时空中存在一个曲率无限的大的点——“时空奇点”①。后来,钱德拉塞卡、朗道和奥本海默等对于大质量恒星演化的研究表明:球对称的大质量恒星在其核燃料燃烧耗尽之后将会不可避免地塌缩成为一个黑洞,从而导致时空奇点的形成(如图1所示)。由于在广义相对论中时空的曲率具有可观测效应,物理学上这种具有可观测效应的无限大并不是物理学家所乐见的。因为在物理世界中并不存在什么真正的无限大。一个理论预言了“无限大”往往预示着这个理论的危机。
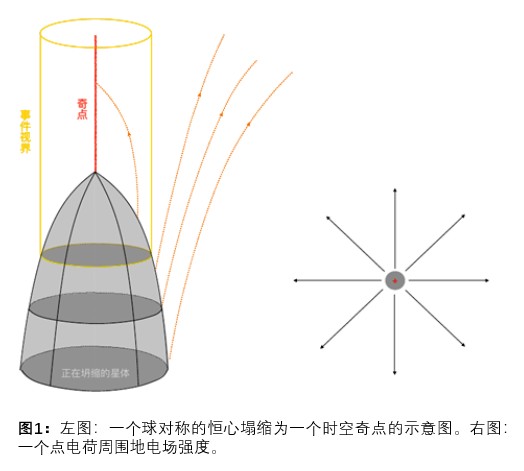
事实上广义相对论的奇点疑难几乎与广义相对论同时诞生。然而在广义相对论研究早期,包括爱因斯坦在内的许多物理学家并不认为在广义相对论的框架下奇点会出现在真实的世界中。首先,施瓦西解和恒星晚期的演化都假设了球对称性,但是真实的星体不可能具有那样精确的球对称性。其次,在弗里德曼-勒梅特-罗伯逊-沃尔克度规里,人们则假设了宇宙是均匀且各向同性的,但是真实的宇宙不可能具有理论模型中那样完美的均匀对称性。这使得一些物理学家认为真实的物理世界并不存在奇点。这一想法非常地自然。比如,在经典电磁学里一个点电荷的电场强度在中心处也是发散的,但是这并不导致经典电磁学的任何危机——因为现实世界里不存在一个真正的“点”电荷。那么在广义相对论里发现的那些“无穷大”也是因为模型过于简化所致吗?对于“球对称”的偏离可以有效地避免时空奇点的产生吗?对于这一个问题的回答分为两派:一派认为“发散”的出现是因为我们采用了过分理想、以至于现实中不存在的模型,其代表人物就包括苏联物理学家栗弗席兹(Lifshitz)和卡拉特尼科夫(Khalatnikov)等人;另外一派则认为在广义相对论框架下时空的奇点是不可避免的,其代表人物就是彭罗斯以及二年前去世的史蒂芬·霍金(Stephen Hawking)。
经过几年的研究,最终彭罗斯和霍金的观点胜出。这其中彭罗斯的数学背景起到了关键作用。1965 年彭罗斯给出了第一个奇异性定理(也称为奇点定理) 的证明[2]。这一工作是里程碑式的。它首次在不依赖对称性的情况下证明了:只要时空中的物质是由一些“正常”的物质构成②,并且时空满足一些基本的性质③,那么时空的奇点是普遍存在,是不可避免地。在证明奇异性定理的过程中,彭罗斯引入了现代广义相对论研究中的许多重要概念,比如时空的奇异性、俘获面、柯西面和时空的整体双曲性等数学概念;并进一步发展了在描述时空整体因果结构极为有用的“彭罗斯图”。这些数学概念与工具的发明极大地澄清了广义相对论中的许多内容,奠定了广义相对论中关于奇异性研究的基调,并在当代已经成为研究广义相对论的标准语言。彭罗斯的这一篇开创性工作一经问世就迅速地吸引了许多物理学家的注意,这其中最为突出的就是霍金。实际上1965年的文章只是彭罗斯一系列关于奇点定理的文章的开篇。在其后的系列研究工作中,彭罗斯和霍金合作对彭罗斯1965年的结果进行了推广,并应用到宇宙学中证明了大爆炸奇点的普遍存在性[3,4]。至此彭罗斯和霍金等人彻底地回答了广义相对论中奇点的存在性问题:对球对称性的偏离并不能有效地克服奇点的产生,奇点的形成在广义相对论中几乎是不可避免的。
三、宇宙监督假设
在意识到奇点的不可避免性后,奇点附近的行为成为物理学家,尤其是广义相对论研究者需要面对一个棘手的问题。在奇点附近,将会出现各种“诡异”的现象。例如:奇点附近大量物质的产生;另外,裸奇点的存在甚至会影响到无限远处的观测者。如何避免这种不良的影响?为此,在1968年到1969年间,彭罗斯提出了弱宇宙监督假设:奇点总是被一个称为“黑洞事件视界”的表面所包裹,因此不再裸露,遥远的观测者不再受其影响[2,5,12]。
在广义相对论的研究中,人们通常将事件视界定义为一个黑洞的边界。事件视界独特的性质使得其两侧的物理世界是因果隔绝的。由于人们是生活在黑洞的外面,如果所有的奇点都隐藏在黑洞的内部的话,那么奇点的存在就不会对我们所能够观测到的物理世界产生任何影响了。这就从一定意义上解决了奇点导致的各种破坏性问题。基于彭罗斯的“奇点普遍存在”的结论和“弱宇宙监督假设”,人们可以作如下思考:物理上可以产生的奇点必须包裹在一个事件视界中。由于宇宙中物质演化产生奇点是普遍存在的,这些奇点都应该隐藏在黑洞的事件视界中,因此黑洞的形成也一定是普遍的。这就是说,在广义相对论中物质的演化必然导致黑洞的出现。弱宇宙监督假设成立的与否对广义相对论自身和天体物理研究具有重要意义。弱宇宙监督假如果成立,那么大质量星体的最终归宿只能是黑洞。
例如,人们发现的第一个时空奇点——施瓦西黑洞的奇点。对于这样的奇点, 奇点的外部的确存在一个被称之为“事件视界”的边界。这一个边界将施瓦西黑洞中奇点包裹起来,如图2所示。事件视界完美地将施瓦西黑洞的奇点隐藏了起来,使得在奇点处任何破坏物理的怪异行为都不会对生活在视界外部的人们产生影响。从这个角度来说的话,施瓦西黑洞的奇点是一个“无害”的奇点。如图2所示。对于已发现的大部分精确解,彭罗斯的弱宇宙监督假设都能被满足。另外,研究表明:在一般条件下,普通物质④组成的球对称的塌缩星体形成的黑洞,奇点也会被视界所包裹。
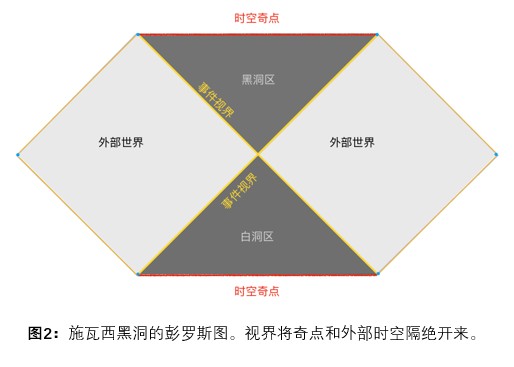
然而,对这样一些特例适用的解决方案到底有多大的普遍性呢?这就是需要人们对弱宇宙监督假设进行证明。和彭罗斯证明奇点定理不同,宇宙监督假设是一个相当困难地问题,到目前为止仍然没有获得完全解决。事实上,黑洞视界定义本身就与时空的整体演化有着密切关系,不像奇点的定义那样局域,这自然也导致对宇宙监督的证明要比奇点困难得多。
鉴于宇宙监督假设如此重要,在无法直接解决这一个问题的情况下,人们试图对这一个问题进行“旁敲侧击”。彭罗斯本人就曾提出过两个思想实验来验证宇宙监督假设。其中一个就是考虑可否通过一些物理允许的过程将一个黑洞“摧毁”但是却保留黑洞内部的奇点。实际上不难发现,如果宇宙监督假设正确,那么这样的过程就不会存在。因此,如果有人能够设计一个物理过程(哪怕只是理论上可行)来“摧毁”黑洞并使得奇点暴露出来,那么他就否定了宇宙监督假设;相反,如果人们在尝试各种努力之后仍然无法摧毁黑洞,那么就从一定程度上暗示了宇宙监督假设的正确性。经过几十年的努力,人们确实在理论上没有发现摧毁黑洞的方法。这在很大程度上坚定了人们对宇宙监督假设的信心。彭罗斯本人提出的第二个思想实验是考虑黑洞的视界面积大小,他发现如果宇宙监督假设成立的话,任何一个黑洞的视界面积都不会比相同质量的施瓦西黑洞的视界面积大。这一个不等式在被提出后就吸引了许多数学和物理学家的兴趣。Trudinger,Gibbons,Geroch,Wald 和Jang 等人在这个不等式或改进型不等式的证明中都做出了重要贡献。在彭罗斯提出这一结论20多年后,也就是2001年,数学家在证明这个不等式上取得了重要进展,证明了一大类情况下黑洞的视界面积确实不会比同样质量的施瓦西黑洞的视界面积大。不过,这个不等式的更一般情况下是否也成立目前还是一个尚未解决的问题。除了这两个思想实验外,人们也可以研究黑洞视界在扰动下的稳定性。这个可以看成是在微扰意义下研究是否可以“摧毁”黑洞。若黑洞事件视界在微扰下不稳定,则奇点可能裸露在视界外部。因此关于黑洞稳定性的研究可以从另一个侧面检验宇宙监督假设[11]。一系列研究表明[12-15]:在线性微扰下,大部分黑洞都是稳定的。因此奇点不会因为线性微扰而从视界内部裸露出来。实际上最近LIGO观测到的双黑洞合并产生的引力波[16]以及“事件视界望远镜”(Event Horizon Telescope)[17,18]对黑洞的直接成像都从实验上验证了黑洞的稳定性,因为倘若黑洞视界不稳定,实验上就不可能观测到黑洞存在的证据了。
另外奇点的存在使得人们无法有效地预言时空中物理现象的演化[5-7]。广义相对论的一个重要物理意义就在于它能够计算并且预言时空的演化,但是奇点的出现破坏了这种可预言性。这对于广义相对论来说是一个致命的挑战。那么有什么机制能够消除或者至少是减弱这种挑战呢?为此彭罗斯提出了一个强宇宙监督假设:物理的时空都是可预测的。彭罗斯的工作表明奇点在经典广义相对论中是不可避免的,为了使视界内的观测者也无法观测到奇点,这就要求奇点必须是类空的(类空奇点的一个例子是前文提到的施瓦西黑洞的奇点)。虽然人们可以依据广义相对论预知其存在,但只有当真正撞上时才能 “观测” 到这样的奇点。关于强宇宙监督的研究也是近几年的前沿热点,本文的作者近期的一个工作证明了对一大类黑洞其奇点一定是类空的[19],算是对强宇宙监督“添砖加瓦”。
四、结束语
在广义相对论提出一百多年来,彭罗斯的关于奇点的一系列开创性工作仍然被认为是自爱因斯坦以来对广义相对论最重要的贡献之一。正如诺贝尔物理学奖委员会主席大卫·哈维兰说“今年获奖者的发现为致密和超大质量物体的研究开辟了新天地。但是,这些奇异的物体仍然提出了许多问题,这些问题需要解答,并激励了未来的研究”。彭罗斯等人获得诺贝尔奖并不意味着他们的研究领域已经“盖棺定论”。相反,关于引力、时空以及宇宙中的那些超大致密天体的研究仍然有着太多的未解之谜等着人们去探索。譬如黑洞的内部结构,黑洞外的引力场检验等问题。不过稍微有些遗憾的是,彭罗斯昔日的研究搭档,曾经提出过著名的“黑洞蒸发”理论,开创了黑洞热力学研究的先河,并因为奇点相关研究工作而与彭罗斯一起获得1988年“沃尔夫奖”的著名物理学家史蒂芬·霍金已经于两年前去世,未能见证这一荣耀的时刻。
注解:
① 这里说的曲率无限大确切地说是由曲率张量构成某些标量是无限大的。这种类型的奇点称作“曲率奇点”。实际上除了曲率奇点外,在广义相对论中还有许多其他形式的奇点,比如“测地不完备”奇点。有一些时空奇点处曲率并不发散。详情可以参阅文献[1]。
② 这里所说的“正常物质”是指它们满足某些“能量条件”。
③ 在彭罗斯最早的证明中要求时空满足“整体双曲性”;后来这个条件被放宽为满足“编时条件”[3,4]。
④ 在某些特殊的情况下,球对称的引力塌缩也可能导致裸露在视界外的奇点[8-10]。
参考文献:
[1] 梁灿彬,周彬, 《微分几何入门与广义相对论》(上册),第二版,科学出版社;
[2] R. Penrose, Gravitational Collapse and Space-Time Singularities, Phys. Rev. Lett. 14, 1965;
[3] S. Hawking, G. Ellis, The Large-Scale Structure of Space-time, Cambridge University Press, Cambridge, 1973;
[4] S. Hawking, R. Penrose, The singularities of gravitational collapse and cosmology, Proc. R. Soc. London A 314, 529;
[5] R. Penrose, Singularities of Spacetime, in Theoretical Principles in Astrophysics and Relativity, edited by N.R. Lebovitz, W. H. Reid, P.O.Vandervoort, 1978;
[6] R. Penrose, Singularites and time-asymmetry, in General relativity, and Einstein centenary survey, edited by S.W.Hawking and W. Israel(1979);
[7] R.M. Wald, Gravitational Collapse and Cosmic Censorship, 1997;
[8] T.P. Singh, Gravitational Collapse and Cosmic Censorship, in Classical and Quantum Aspects of Gravitation and Cosmology. Edited by G. Date and B.R. Iyer. 1996;
[9] M. W. Choptuik, Phys. Rev. Lett. 70 9 (1993).
[10] D. Christodoulou, Commun. Math. Phys. 105 337, 106 587(1986); 109 591,109 613(1987).
[11] R. Penrose, The Question of Cosmic Censorship, J. Astrophys. Astr. (1999) 20, 233–248;
[12] C.V. Vishveshwara, Nature, 227, 936–938, (1970);
[13] R.H. Price, Phys. Rev. D, 5, 2419–2438, (1972);
[14] R. M. Wald, Journal of Mathematical Physics 20, 1056 (1979);
[15] B S Kay and R M Wald, Class. Quantum Grav. 4 893, 1987;
[16] B. Abbott et al., “Observation of Gravitational Waves from a Binary Black Hole Merger,” Phys. Rev. Lett. 116(6)(2016)061102;
[17] K. Akiyama et al., “First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole,” Astrophys. J. L1(1)(2019)875;
[18] K. Akiyama et al., “First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole,” Astrophys. J. L4(1)(2019)875.
[19] R.G. Cai, L. Li, R.Q. Yang, No Inner-Horizon Theorem for Black Holes with Charged Scalar Hair, [arXiv:2009.05520 [gr-qc]].
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
喜欢就支持一下吧











暂无评论内容