时空转换是空间与时间概念的转化,与时空概念的与远近、长短、快慢、动静等有关。
- 中文名
- 时空转换
- 外文名
- Time and space conversion
- 描 述
- 空间与时间概念的转化
- 应 用
- 测量方法
- 学 科
- 物理
目录
- 1 概念
- 2 基于时空转换的精密位移测量新方法
空间为移动的,转换为时间则为时间则为时间的移动或时间的变动;空间上移动的快慢,转换为时间则指时间上频率的快慢;空间为静止的,则以静止的点位坐标,或转换成时间上已完成,或转换为时间上将要完成。
文献 [1] 中提出的“时空坐标转换”和“时栅位移传感器”,体现了“用时间测量空间”的基本思想,以图改变传统的精密位移测量方法和传感器总是依赖于精密刻划加工的传统思路,改由更廉价、手段更多样化的时间量来精密测量位移。在研制过程中一个敏感的问题是:这种方法与传统的比相方法尤其是利用时钟脉冲插补的比相方法是一回事吗?
传统的精密位移测量方法
(1)非调制方法
典型传感器为光栅,其求取位移的数学模型为:x=∫vdt=∫(dx/dt)dt=∫dx=∑Δx=∑W=W∑Px
上式说明,由于运动物体的运动速度v是非解析的(可能是快慢不定、忽动忽停、正反变向等),积分无法完成,于是变通为求微位移dx来完成。各种栅式传感器如光栅等,就是通过制造微位移Δx(即栅距W),再经光电转换成为电脉冲Px,利用计数电路累加微位移而得到总位移x。为此需要W尽量细微,且每一个W都要精确。
(2)调制方法
典型传感器为感应同步器,其电信号表达式为:u=Asin(Kt+Δh)=Asin(Kt+(2π/W)x)
它表明相位角Δh在1个节距W内与动尺和定尺的相对位移x有一一对应关系,每经过1个节距,变化1个周期2π,而与速度无关。通过2路信号的相位比较,得到相位之差,再换算出位移量。
文献 [1] 还介绍了另一种工作于调制方法的传感器——齿栅的原理,以及用2列火车的“思想实验”所作的推导。这可视为以运动的方法将非调制式传感器用于调制工作方式,数学模型与公式是一样的,文献 [1] 将其分别称之为“动激型”和“电激型”,并且将这个典型的行波表达式推导成为:
u=Asin(Kt+(2π/W)x)=Asin(2πft+(2π/W)x)=Asin2π(t/T+x/W)
此式说明3点:
①式中的时间t和空间x处于完全对等的关系,时间以固定的T为周期,空间x以固定的节距W为周期。
②相位是没有量纲的,因此上式可以任意认为2项中的一项为变化的相位,另一项为固定的初相位,即t或x都可作为自变量。“时空转换”由此而起。
③动激型调制传感器以固定的空间W划分再以恒速V运动,产生出的电信号u具有固定的时间周期T,T=W/V;电激型调制传感器以固定的空间W划分再通以固定时间周期T的电信号,产生恒速运动的行波,行进速度为恒速V,V=W/T。
如果再把式中的x=∫vdt带入,则公式涵盖了调制式与非调制式原理,时间T、t和空间W、x匀速运动V和变速运动v,机械运动和电信号等诸多具有对偶关系的变量,由此构成所提出的“运动坐标系”,引出了下面的讨论。
时栅位移传感器原理
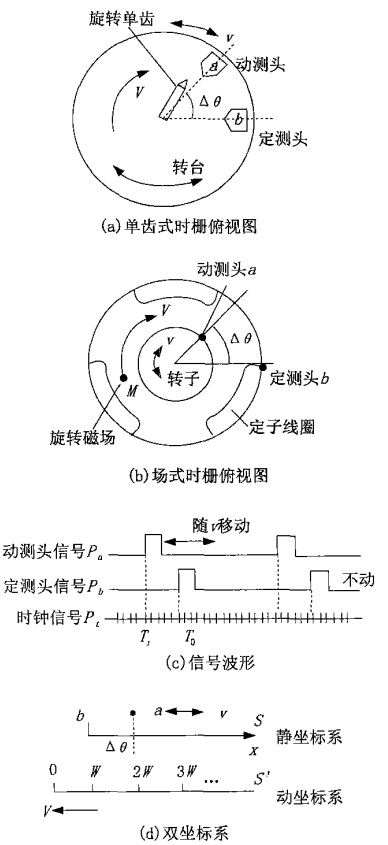 图1 时栅原理图
图1 时栅原理图按照时空坐标转换思想:“建立相对匀速运动双坐标系,则一个坐标系上的位置之差(位移)表现为另一个坐标系上观察到的时间之差”,文献 [1-2] 分别提出了“单齿式时栅”和“场式时栅”的构建原理如图1所示。它们是一种“对偶”的关系,电信号波形图是一样的。
图1(a)以电机带动的恒速V单齿作为运动坐标系,节距W=360°。其缺点在于旋转机械引起的振动和非匀速性,以及体积大和安装不便,尤其是不能测直线位移。图1(b)根据电机原理,由空间互差120°的三相绕组配合时间互差120°的三相电流产生的恒速V旋转磁场M为运动坐标系,匀速性大大改善,体积缩小,安装方便,且根据直线电机原理,直线位移也一样能测。从图1(d)容易看出,无论静坐标系上的运动质点a(动测头)以何种变速度v运动(快慢、动停、正反转等),只要有相对于坐标原点b(定测头)的位移,就会被动坐标系上的间距为W的观察点(单齿或运动磁场的过0点)反复采样确定,Δθ=V(Ti-T0),即位置差等于时间差与恒定因子V的乘积。
时栅与传统的传感器原理比较
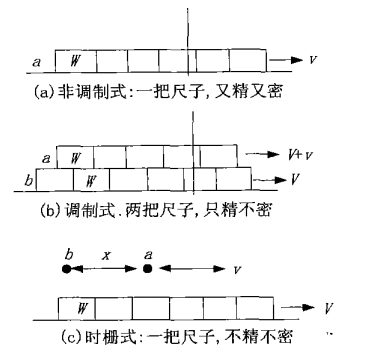 图2 三种测量位移方法的思想实验
图2 三种测量位移方法的思想实验从图1(c)电信号处理的角度看,求Ti和T0的时间差,也就是求Pa和Pb信号的相位差,因此时栅的时间比较方法与调制式传感器的比相方法非常相似,尤其是当调制式传感器比相采用时钟脉冲来插补时,简直就是一回事。这是不是意味着同样的原理换了一种说法呢?
图2(a)用大地标志杆记录火车通过的边沿数,累加值就是总位移,这就是以光栅为代表的非调制式传感器测量原理,x=∑W,因此要求W尽量小,以满足分辨率要求,而用累加满足大量程测量要求。特点是:测量与速度v无关,(或者说与时间无关),与刻划精度紧密相关,每个W必须一样。可概括为“一把尺子,既要密,又要精。”
图2(b)2列火车代表动尺和定尺,测量的位移是a相对于b的位移,而不是相对于大地的位移。这是对以感应同步器为代表的电激型调制式位移传感器原理的一种抽象和解释,而对以齿栅为代表的动激型调制式传感器就更形象一些,容易理解一些,标志杆不是对火车边沿记数,而是分别记录2列火车的边沿到达标志杆的时间Ti和T0。只要a、b火车有相对位移,Ti和T0之差ΔT就会发生变化,这种变化是以“比相”的方式求出的,可以用分辨率很高的时钟脉冲插补来实现,因此不需要W很小也可以满足分辨率要求,但必须保持W一致。可以设想,如果W不一致,本来a、b没有相对位移,由于ΔW的存在,测出ΔT发生变化,就以为发生了位移,也就是产生了误差。调制式传感器如感应同步器、旋转变压器的W都比较大,但刻划精度要求很高,是制约其精度和成本的主要因素。这种原理可概括为“两把尺子,不要密,但要精”。
图2(c)即图1(d)的原理。对于时栅来说,首先,它不要2列火车,就是说不要动、定2把尺子,也就谈不上相位“比较”即“比相”,换言之,时栅绝不是比相,而是只要一把尺子进行“扫描”的一种概念:运动坐标系上的每一个节点(观察者序列)不断对参考点b和运动质点a进行扫描采样得到Ti和T02组时间序列,只要有位移x,就会从Ti和T0的时间差上反映出来。这就是文献 [1] 提出的所谓时空坐标转换理论,其核心思想及其内涵可以概括为3句话:
(1)建立带时间考察点的相对匀速运动双坐标系,则一个坐标系上的位置之差(位移),表现为另一个坐标系上观察到的时间之差,即x=V(Ti-T0)。
(2)通过建立匀速运动坐标系,把对被测物体的匀速要求,转化为对传感器的匀速要求,使得用时间测变速运动物体的位移空间成为可能。
(3)在一个匀速运动坐标系中,时间(时钟脉冲)具有了惟一的空间当量,就是V。
其次,这种方法不要求采样节点序列均匀分布,节距W一致也好,不一致也好,不引入刻划误差。若W保持一致,采得的是连续的位移曲线x(t)上的一组离散的点;若W不一致,采得的是x(t)上的另一组离散的点,它们都能反映x(t)的变化规律,不存在由采样方法和刻线尺的刻划误差而引起的测量误差,这是时栅与传统测量方法最大的区别和优势。并且只要提高V,就可以满足任何采样频率的要求。因此,这种原理可以概括为“一把尺子,既不要密,也不要精”。
时空坐标转换方法与比相方法的另一个本质区别在于对刻线尺的运动速度要求。时栅传感器不要求尺子刻线精和密,但要求尺子运动速度V必须恒定,即是把对传感器的机械问题,转化成为电气问题(而研制者认为人类解决基于时间的电气问题的手段比解决基于空间的机械问题的手段要多得多、先进得多)。而比相方法则不一定。如果是传感器内的2把尺子在比相,它也必须保持V恒定。文献 [1] 中的齿栅就要求电机转速恒定;而对感应同步器来说,虽然没有看得见的转动,却有恒定的节距W和周期T,也就有一个广义的恒定速度或者行波速度V=W/T。但是如果用2把图2(a)的尺子来进行比相,最典型的例子就是机床传动链2端的传动误差的测量,那是一种“同步位移比较”的概念,并不要求运动速度恒定。例如无论机床(如滚齿机)电机运动速度恒定与否,对传动链2端的运动进行比相式测量,即可测出机床传动误差。可概括为“时栅要求尺子恒速,比相则有时恒速,有时不恒速”。
综上所述,从理论层面上说,时空坐标转换方法是对传统调制式位移测量方法的一种沿续和提高。一方面它可以用“以时间测空间”的思想解释任何一种调制式传感器,从而从新的角度赋予其新的内涵。另一方面,它可以在此思想的指导下,发明设计出各种全新的更先进的传感器。从技术层面上说,时栅位移传感器因为彻底摒弃了以精细刻划为代表的精密机械加工而具有重要实用价值。一方面其生产成本可以大大降低而具有商品化竞争力,另一方面因不在乎生产现场的碰撞、油污的干扰而使传感器不仅可作为计量基准,也可作为生产基准,“价格低廉,使用随意”,这正是人们对精密位移测量手段的永恒追求。 [3]
词条图册更多图册

概述图册(2)
- 参考资料
-
- 1. 彭东林, 刘成康, 谭为民. 时空坐标转换理论与时栅位移传感器研究[J]. 仪器仪表学报, 2000, 21(4):340-342 .知网.2000[引用日期2018-08-20]
- 2. 彭东林, 张兴红, 刘小康,等. 场式时栅位移传感器研究[J]. 仪器仪表学报, 2003, 24(3):321-323 .知网.2003[引用日期2018-08-20]
- 3. 彭东林, 张兴红, 刘小康,等. 基于时空转换的精密位移测量新方法与传统方法的比较[J]. 仪器仪表学报, 2006, 27(4):423-426 .知网.2006[引用日期2018-08-20]
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END











暂无评论内容